Retas Numéricas
13 de fevereiro de 2023Equação do 2º grau do tipo ax2 = b
22 de fevereiro de 2023
(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1º grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.
Sistema de Equações
Um sistema de equações nada mais é do que o conjunto de equações polinomiais que são consideradas simultaneamente para sua resolução. Um sistema é utilizado para a resolução de problemas que envolvam duas ou mais variáveis.
Já um sistemas de equações polinomiais de 1º grau é formado por duas equações de 1º grau com duas diferentes incógnitas cada uma.
Um sistema de equações do 1º grau é representado da seguinte forma:
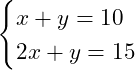
Resolução pelo método da substituição
Um dos métodos de resolução de um sistema de equações de 1º grau (talvez o mais recorrido), é o da substituição. Ele consiste em isolar uma das incógnitas e substituí-la na outra equação.
Retornando ao exemplo anterior, podemos isolar tanto 
quanto 
. Então iremos isolar
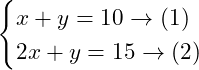
Agora substituindo (1) em (2), teremos:
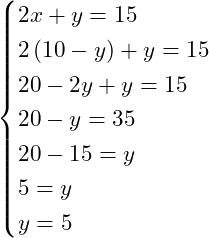
Uma vez encontrado o valor de uma das incógnitas, neste caso o , voltamos a substituí-lo em (1) ou em (2).
Substituindo em (1), teremos:
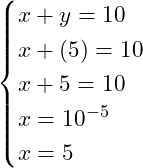
Desta forma encontramos os valores das incógnitas. Sendo 
e 
. Ou ainda na forma do conjunto solução 
.
Resolução pelo método da adição
A resolução pelo método da adição consiste em adicionar as duas equações de tal forma que a soma de uma das incógnitas seja igual a zero. Para isso, pode ser necessário multiplicar uma ou as duas equações para que a soma de uma das incógnitas seja igual a zero.
Retornando ao nosso exemplo anterior, vamos multiplicar a equação (1) por 
para que mude de sinal.
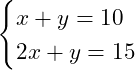
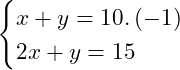
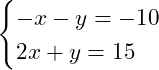
Fazendo a adição das duas equações: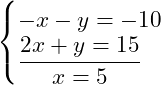
Assim como no método de substituição, agora basta substituir o valor encontrado () em uma das equações e encontrar o valor de .
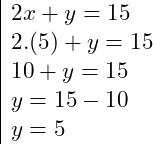
Desta forma determinamos os valores para e . Ou no conjunto solução:
Exercícios
ENEM – exercícios
REsolução
ENEM – Exercício
Resolução
Continua depois da publicidade
Gostou deste conteúdo? Compartilhe agora mesmo!
