Potenciação e Radiciação

Múltiplos e Submúltiplos

16 de janeiro de 2023

O princípio multiplicativo da contagem

18 de janeiro de 2023

16 de janeiro de 2023

(EF08MA02) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.

Potenciação
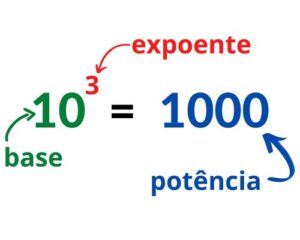
Propriedades de potenciação
Radiciação
Propriedades da radiciação
Operações com radicais

Potenciação

A Potenciação é uma forma de escrever números muito grandes como potências. Ou seja, quando este número é multiplicado por ele mesmo diversas vezes, pode-se substituí-lo por uma base (número que se repete) elevado a um expoente (número de repetições).

10³ = 10 × 10 × 10 = 1.000

Na forma algébrica podemos representar da seguinte maneira:

$a^{n}=\underset{n \ vezes}{\underbrace{a \cdot a \cdot … \cdot a }}$

A expressão acima pode ser lida como sendo “a” elevado a potência “n”. Ou simplesmente “a” elevado a “n”. Aqui a é a base e n o expoente e o resultado a potência.

Conheça nossos planos de aulas online

Atenção

Todo número natural elevado à primeira potência tem como resultado ele mesmo, por exemplo, 5¹=5

Todo número natural (diferente de zero) quando elevado a zero, tem como resultado 1, por exemplo, 5⁰= 1

Todo número negativo elevado a um expoente par tem resultado positivo, por exemplo, (-5)²= 25

Todo número negativo elevado a um expoente ímpar tem resultado negativo, por exemplo, (-5)³= 125

Propriedades de Potenciação

Expoente Zero

Uma base elevada a um expoente igual a zero ( 0 ), independente do seu valor, sempre terá uma potência igual a 1. Com a pertencente aos números reais, com a ≠ 0

a⁰ = 1

$1 = \frac{a^m}{a^m} = a^{m-m}=x^0$

Expoente unitário ( 1 )

Uma base elevada a um expoente unitário ( 1 ), independente do seu valor, sempre terá como resultado uma potência cujo valor será igual a própria base. Com a pertencente aos números reais, com a ≠ 0

a¹ = a

Potência da potência

É quando uma potência é a base de outra potência. Mantem-se a base e multiplica-se os expoentes.

Com a pertencente aos números reais e com a ≠ 0, e m e n pertencente ao conjunto dos números naturais.

(a^m)ⁿ = a^m*n

Produto de potências de mesma base

O resultado deste produto entre duas potências de bases iguais, será um terceira potência de mesma base, na qual o expoente será a soma dos expoentes das potências que estão sendo multiplicadas.

Com a pertencente aos números reais e com a ≠ 0, e m e n pertencente ao conjunto dos números naturais.

a^m * aⁿ = a^{m + n}

Divisão de potências de mesma base

O resultado da divisão de potências de mesma base, será a manutenção da base e a subtração dos expoentes.

Com a pertencente aos números reais e com a ≠ 0, e m e n pertencente ao conjunto dos números naturais.

a^m : aⁿ = a^{m – n}

$\begin{align*}\frac{x^a}{x^b} &= \frac{\quad \overbrace{x \times \cdots \times x}^{a \text{ vezes}}\quad}{\underbrace{x \times \cdots \times x}_{b \text{ vezes}}}\\[0.2cm] &= \frac{\quad \overbrace{x \times \cdots \times x}^{a-b \text{ vezes}}\times\overbrace{\cancel{x \times \cdots \times x}}^{b \text{ vezes}}\quad}{\underbrace{\cancel{x \times \cdots \times x}}_{b \text{ vezes}}}\\[0.2cm] &= \underbrace{x \times \cdots \times x}_{a-b \text{ vezes}}\\[0.2cm] &=x^{a-b}\end{align*}$

Potência cuja base é um produto

Quanto temos um produto de dois números (base) elevados a um expoente, cada uma das bases deverá ser elevados separadamente ao expoente da potência.

Com a e b pertencente aos números reais e com a e b ≠ 0, e m e n pertencente ao conjunto dos números naturais.

(a.b)^m = a^m. b^m

Potência cuja base é uma divisão

Quanto temos uma divisão de dois números (base) elevados a um expoente, cada uma das bases deverá ser elevados separadamente ao expoente da potência.

Com a e b pertencente aos números reais e com a e b ≠ 0, e m e n pertencente ao conjunto dos números naturais.

(a ÷ b)^m = a^m ÷ b^m

$\begin{gather*} \left(\frac{a}{b}\right)^m = \frac{a^m}{b^m} \end{gather*}$

Expoente negativo

Uma potência com expoente negativo é igual ao inverso da base, elevado ao expoente com seu sinal também invertido.

Com a pertencente aos números reais e com a ≠ 0, e n pertencente ao conjunto dos números naturais e diferente de zero.

$a^{-n}=\left( \dfrac{1}{a}\right) ^{n}$

Expoente racional

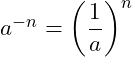
Uma potência com expoente racional pode ser escrita como raiz enésima de a elevado a m.

$a^{\frac{m}{n}}=\sqrt[n] {a^{m}}$

Continua depois da publicidade

Propriedades de Potenciação

Propriedades	Fórmula	Exemplo
Expoente zero	a⁰ = 1	5⁰ = 1
Expoente unitário	a¹ = a	5¹ = 5
Potência da Potência	(a^m)ⁿ = a^m*n	(5²)³ = 5^{2 x 3} = 5⁶
Produto de potências de mesma base	a^m * aⁿ = a^{m + n}	5²* 5³ =5²⁺³ =5⁵
Divisão de potências de mesma base	a^m : aⁿ = a^{m – n}	5⁵ : 5³ = 5^5-3= 5²
Potência cuja base é um produto	(a.b)^m = a^m. b^m	(5 * 2 )³ = 5³. 2³
Potência cuja base é uma divisão	(a÷b)^m = a^m÷ b^m	(5÷2)³ =5³÷2³
Expoente negativo	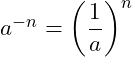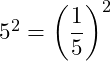$a^{-n}=\left( \dfrac{1}{a}\right) ^{n}$	$5^{2}=\left( \dfrac{1}{5}\right) ^{2}$
Potência com expoente racional	$a^{\frac{m}{n}}=\sqrt[n] {a^{m}}$	$5^{\frac{2}{3}}=\sqrt[3] {a^{2}}$

Radiciação

A radiciação é o cálculo de um número que elevado a um expoente produz o resultado inverso que se obtém na potenciação.

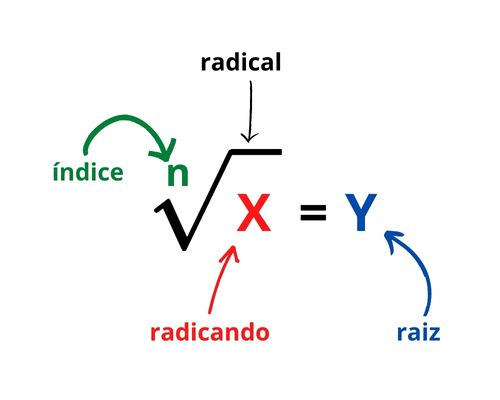
Ou em outras palavras, com a radiciação podemos encontrar a raiz enésima de um número “x”.

Quando o índice for igual a 2 (raiz quadrada), não é necessário representar o algarismo 2.

A potenciação e a radiciação são operações inversas. Assim, é fundamental saber a correção entre elas para poder resolvê-las.

$\sqrt[n]{a}=b\rightarrow b^n=a$

Exemplo 1

$\sqrt[2]{9}=3\rightarrow3^2=9$

Exemplo 2

$\sqrt[3]{8}=2\rightarrow2^3=8$

Exemplo 3

$\sqrt[4]{16}=2\rightarrow2^4=16$

Propriedades da radiciação

Raiz enésima de a elevado a n é igual a “a”

A raiz enésima de um numero a elevado a n será o próprio número a. Ou seja, quando o índice da raiz e o expoente foram números iguais, a raiz é o próprio radicando.

$\sqrt[n]{a^n}=a$

$\sqrt[4]{2^4}=2$

A raiz do produto é igual ao produto das raízes

O radicando formado pela multiplicação de dois números será igual ao produto das raízes destes números.

$\sqrt[n]{a . b}= \sqrt[n]{a} . \sqrt[n]{b}$

$\sqrt[3]{3 . 2}= \sqrt[3]{3} . \sqrt[3]{2}$

A raiz do quociente é igual ao quociente das raízes

Esta propriedade é tal qual do produto, salvo o fato de ser neste caso divisão. Ou seja, o radicando sendo dois números que estão sendo divididos entre si, será igual ao quociente das raízes.

$\sqrt[n]{a : b}= \sqrt[n]{a} : \sqrt[n]{b}$

$\sqrt[3]{3 : 2}= \sqrt[3]{3} : \sqrt[3]{2}$

A mesma propriedade é válida para frações

$\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$

Raiz da raiz

A raiz de uma raiz pode ser resolvida passo a Passo, ou ainda multiplicando o índice dessas raízes.

$\sqrt[n]{\sqrt[m]{a}}=\sqrt[n\cdot m]{a}$

Potência de uma raiz

Quando uma raiz é elevada a um expoente x, o radicando também é elevado ao mesmo expoente.

$\left(\sqrt[n]{a}\right)^x=\sqrt[n]{a^x}$

Divisão e Multiplicação do expoente com o índice

Podemos dividir e multiplicar o expoente do radicando e o radical por um mesmo número

$\sqrt[n]{a^m}=\sqrt[n:b]{a^{m:b}}$

$\sqrt[n]{a^m}=\sqrt[n\cdot b]{a^{m\cdot b}}$

Radiciação para potenciação

uma radiciação pode ser escrita na forma de potenciação

$\sqrt[n]{a^m}=a^\frac{m}{n}$

Simplificação de radicais

Para raízes não exatas, é possível simplificar o radical escrevendo-o da forma mais simples possível. Esta simplificação é feita fatorando o radicando.

Exemplo:

Determine a seguinte raiz: $\sqrt{242}$

$\begin{array} {r | l}242 & 02\\121 & 11\\11 & 11 \\1 & \\& \\& 2 . 11^{2}\end{array}$

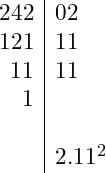
Assim temos:

$\sqrt{242}=\sqrt{2 \cdot 11^2}$

e então:

$\sqrt{242}=\sqrt{2} \cdot \sqrt{11^2}$

E então resolvendo a raiz $\sqrt{11^2} = 11$

Temos por fim:

$\sqrt{242}=11\sqrt2$

Operações com radicais

Adição e Subtração

Quando temos o mesmo radical, conserva-se o radical e soma-se ou subtrai-se os coeficientes.

$2\sqrt3+3\sqrt3=5\sqrt3$

Quando o radical é diferente, não pode-se fazer a soma dos mesmos. Assim, pode-se, se necessário, encontrar o valor aproximado das raízes.

Divisão e Multiplicação

Se o radical tiver o mesmo índice, faz-se a operação de divisão ou multiplicação dos radicandos mantendo o radical.

$\sqrt[3]{2}\cdot\sqrt[3]{3}=\sqrt[3]{2\cdot3}=\sqrt[3]{6}$

Quando o radical é diferente, primeiro é necessário igualar os índices. Seja pela multiplicação ou divisão do radicando e o índice.

Exemplo:

$\sqrt[3]{2} \cdot\sqrt[2]{2}$

$\sqrt[3\cdot2]{{2}^2\ } \cdot \sqrt[2\cdot3]{2^3}$

$\sqrt[6]{{2}^2 \cdot 2^3}$

$\sqrt[6]{4 \cdot 8}$

$\sqrt[6]{32}$

Exercícios

ENEM – exercícios

Resolução

REsolução

ENEM – Exercício

Resolução

Não se esqueça:

Lembre-se que pelas propriedades de potenciação que, todo número elado a zero é igual a 1, e todo número elevado a 1, é ele mesmo.

Continua depois da publicidade

Gostou deste conteúdo? Compartilhe agora mesmo!

Fernando Pitt

Engenheiro, Mestre, Professor, Educador, e um entusiasta de tecnologia.

10² = 10 · 10 = 100	$\sqrt[2]{100}=10\rightarrow 10^2=100$
10³ = 10 · 10 · 10 = 1.000	$\sqrt[3]{1000}=10\rightarrow 10^3=1000$
10⁴ = 10 · 10· 10· 10 = 10.000	$\sqrt[4]{10000}=10\rightarrow 10^4=10000$
10⁵ = 10· 10· 10· 10· 10 = 100.000	$\sqrt[5]{100000}=10\rightarrow 10^5=100000$

Potenciação e Radiciação

Múltiplos e Submúltiplos

O princípio multiplicativo da contagem