O princípio multiplicativo da contagem
18 de janeiro de 2023ChatGPT: será o fim dos professores de redação?
31 de janeiro de 2023
(EF08MA04) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.
Porcentagem
Representação da porcentagem
Como calcular um valor percentual
Aplicação prática de porcentagem
Exercícios
Porcentagem
A utilização de cálculos de porcentagem está presente no dia a dia das pessoas de uma forma tão intensa, que muitos nem percebem isso. E mesmo assim costumam dizer que não gostam ou não sabem nada sobre porcentagem.
Mas porcentagem nada mais é do que uma medida de razão com base 100. Dai o seu nome: “Por Cem”. Cujo símbolo é ( % ). Ou ainda, podemos afirmar que porcentagem é o cálculo para descobrir a proporção entre uma ou mais partes em relação ao “todo”.
Formas de representação de Porcentagem
Embora a forma mais comum de representação de uma porcentagem seja com a utilização do símbolo (%), existem outras.
Forma Percentual: é a representação utilizando o símbolo de porcentagem (%):
22%
Forma fracionária: A forma fracionária é uma das primeiras que aprendemos, ainda no 5º ano. E nada mais é do que a representação da parte (numerador) em relação ao todo (denominador). Este denominador geralmente igualado a 100. Por exemplo, 22% seria representado na forma fracionária da seguinte maneira:
Forma Decimal: Já a forma decimal é calculada pela divisão da parte (numerador) pelo todo (denominador), e é geralmente representada por meio de vírgula. 
Sempre que a representação decimal de um número percentual for igual a um ( = 1 ), significa que a parte (numerador) corresponde ao todo (denominador), ou seja, 100%. Pois:
Observe que existe um outro símbolo muito parecido que pode gerar dúvidas aos desatentos. Que é o “por mil”. Neste caso a razão terá como base o número 1.000 (mil) e será representada por: ‰
22 ‰ 
Como calcular um valor percentual
Este método muito simples e prático pode ser utilizando tanto manualmente quanto com o auxílio de máquinas de calcular. Basta dividir o valor percentual (%) por cem, e o número decimal encontrado multiplicá-lo pelo valor cujo percentual deseja-se encontrar.
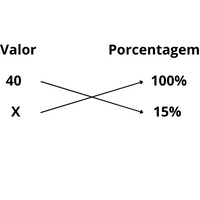
Por exemplo: Qual é o valor de 15% de 40?
O resultado será 6. Ou seja, 15% de 40 é igual a 6.
Seguindo o mesmo exemplo anterior, agora vamos encontrar o valor de 15% de 40 usando a forma fracionária. Para isso, transformamos o valor percentual em uma fração com base 100 (denominador), e simplificamos até encontrarmos uma fração irredutível.
A fração irredutível resultante então é multiplicada pelo valor:
A regra de três é particularmente muito simples de ser resolvida e muito prática. A sua resolução está baseada em considerar o todo como sendo 100%, e então igualar esta razão a outra com a variável que desejamos encontrar, seja ela o valor ou mesmo o percentual deste valor.
Novamente utilizando o exemplo de 15% de 40, temos que o valor 40 corresponde ao 100%, e então montamos a regra de três da seguida forma:
Aplicação prática de porcentagem
No cotidiano são muitas as aplicações práticas envolvendo porcentagem. Como por exemplo, o cálculo de descontos ou mesmo aumentos percentuais. E não raro, em concursos / vestibulares, ENEM e nas provas escolares muitos alunos acabam errando e perdendo pontos preciosos.
É importante destacar que em um cálculo de desconto, encontraremos dois valores. Um é o próprio desconto, e o outro é o valor final. E é aqui que muitos erram.
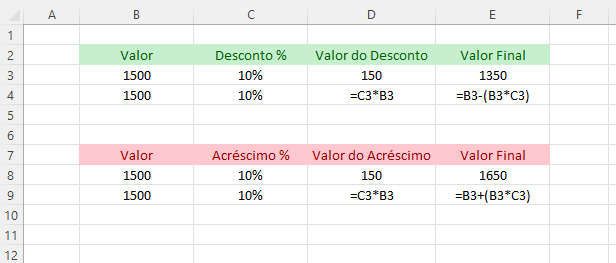
Por exemplo: Qual é o valor que João irá pagar, se ele comprar um produto que custa 1.500 Reais e ele receberá 10% de desconto pelo pagamento à vista.
Observe que neste exemplo o objetivo é encontrar o valor final do pagamento, ou seja, quanto ele irá pagar, mas para isso é necessário calcular o valor do próprio desconto antes. Este cálculo pode ser feito pelo método que você mais domina.
Assim, vamos calcular o valor do desconto inicialmente transformando o percentual em decimal:
Agora multiplicamos o valor decimal (0,1) pelo valor inicial (1.500 Reais) e encontraremos o valor do desconto igual a 150,00 reais.
Por fim, agora basta subtrair o valor do desconto (150 reais) do valor inicial (1.500 reais), e assim encontrar o valor a ser pago de 1.350 reais.
A forma de resolução é idêntica ao cálculo de descontos, salvo que no final em vez de subtrair o valor encontrado, este será adicionado ao valor inicial.
Por exemplo: Utilizando o mesmo exemplo anterior, agora vamos imaginar que João em vez de pagar à vista resolveu pagar a prazo, e por este motivo, terá um aumento no valor correspondente a 10%.
Inicialmente encontraremos o valor correspondente aos 10% em números decimais:
Agora multiplicamos o valor decimal (0,1) pelo valor inicial (1.500 Reais) e encontraremos o valor do acréscimo que será igual a 150,00 reais.
Por fim, agora basta SOMAR o valor do acréscimo (150 reais) do valor inicial (1.500 reais), e assim encontrar o valor a ser pago de 1.650 reais.
Uma forma prática e rápida de calcular o valor final (sem calcular o valor do desconto), é utilizando o fator multiplicativo.
Fator de multiplicação = 1 – percentual de desconto
Por exemplo: Utilizando o mesmo exemplo anterior, no qual João terá um desconto de 10% para o pagamento à vista, inicialmente calculamos em decimal o valor correspondente aos 10%:
O próximo passo é encontrar o fator de multiplicação subtraindo o valor (0,1) de 1 (que corresponde ao todo, ou seja, 100%).
Fator de multiplicação = 1 – 0,1 = 0,9
Por fim, multiplica-se o fator de multiplicação pelo valor inicial, cálculo este que encontrará o resultado direto de 1.350 Reais.
Tal qual o cálculo do desconto, aqui também precisamos transformar o valor percentual para a forma decimal. Seguindo o mesmo exemplo, temos que 10% é igual a 0,1.
Contudo, agora o fator multiplicativo será encontrando SOMANDO este valor a 1 (um).
Fator de multiplicação = 1 – percentual de aumento
Fator de multiplicação = 1 +0,1 = 1,1
Agora multiplicando o valor inicial pelo fator multiplicativo, iremos encontrar o valor final a ser pago de 1.650 reais.
Além de utilizar a calculadora apenas para fazer os cálculos, de acordo com os métodos que apresentamos anteriormente, também é possível utilizá-la para encontrar os valores de forma direta.
O Excel sendo uma planilha eletrônica é capaz de executar praticamente qualquer tipo de cálculo, incluindo porcentagem.
E para isso, basicamente precisamos criar as fórmulas tais quais faríamos utilizando lápis e papel ou mesmo a calculadora.
A seguir está um exemplo de como faríamos para calcular um desconto ou um acréscimo percentual.
Continua depois da publicidade
Exercícios
ENEM 2020 – O quadro representa os gastos mensais, em real, de uma família com internet, mensalidade escolar e mesada do filho.
| Internet | Mensalidade Escolar | Mesada do Filho |
|---|---|---|
| 120 | 700 | 400 |
No início do ano, a internet e a mensalidade escolar tiveram acréscimos, respectivamente, de 20% e 10%. Necessitando manter o valor da despesa mensal total com os itens citados, a família reduzirá a mesada do filho.
a) 15,0
b) 23,5
c) 30,0
d) 70,0
e) 76,5
A resolução deste exercício exige alguns passos:
1º: Calcular o novo valor da internet: vamos fazer isso utilizando o fator multiplicativo.
Como ela aumentou 20%, o que em números decimais corresponde a 0,2. Assim o fator multiplicativo será de F=1+0,2 = 1,2.
Então:
120 x 1,2 = 144 reais será a nova taxa de internet
2º:Calcular o novo valor da mensalidade escolar: também utilizando o fator multiplicativo, temos que 10% em decimais é 0,1, então o fator será F = 1 + 0,1 = 1,1
700 x 1,1 = 770 reais.
3º: Calcular o orçamento total: agora devemos saber qual é o orçamento total que deverá ser mantido, e assim descobrirmos qual é o novo valor da mesada do filho.
Orçamento total = 120 + 700 + 400 = 1.220 (agora substituindo pelos novos valores após o reajuste)
Orçamento total = 144 + 770 + nova mesada = 1.220
Nova mesada = 306 reais (após os reajustes da internet e escola)
Agora utilizando a regra de 3, e considerando que o valor da mesada anterior (400 reais) era o 100%, vamos descobrir qual é o valor que corresponde agora:
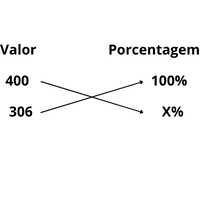
Sabendo que agora a mesada corresponde a somente 76,5% do valor anterior, podemos concluir que a redução da mesma foi de 23,5%, pois:
Resposta B
ENEM – Exercício
Continua depois da publicidade
Gostou deste conteúdo? Compartilhe agora mesmo!
