Sistema de equações do 1º grau
22 de fevereiro de 2023Sequências numéricas
3 de março de 2023
(EF08MA09) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2º grau do tipo ax2 = b.
Equação do 2º grau
Uma equação do 2º grau é caracterizada por um polinômio de grau 2. Ou seja, uma expressão polinomial do tipo ax2+bx+c=0 em que ![]() ,
, ![]() e
e ![]() são números reais (
são números reais (![]() ).
).
A resolução da equação do 2º grau tem como objetivo encontrar os valores de ![]() que tornem a expressão igual a zero (0). Estes valores de
que tornem a expressão igual a zero (0). Estes valores de ![]() são as raízes da equação.
são as raízes da equação.
Equações do 2º grau incompletas
Se uma equação do 2º grau completa é caracterizada ![]() , onde temos o maior expoente de
, onde temos o maior expoente de ![]() igual a 2, uma equação do 2º grau incompleta será aquela em que os coeficientes “b” e/ou “c” serão iguais a zero (
igual a 2, uma equação do 2º grau incompleta será aquela em que os coeficientes “b” e/ou “c” serão iguais a zero (![]() e/ou
e/ou ![]() . Note que o coeficiente “a” sempre deverá ser diferente de zero
. Note que o coeficiente “a” sempre deverá ser diferente de zero ![]() . Pois caso o contrário ela deixará de ser uma equação do 2º grau.
. Pois caso o contrário ela deixará de ser uma equação do 2º grau.
![]() é incompleta, pois
é incompleta, pois ![]() e
e ![]()
![]() é incompleta, pois
é incompleta, pois ![]()
![]() é incompleta, pois
é incompleta, pois ![]()
Resolução das equações do 2º grau incompletas
A resolução de uma equação do 2º grau incompleta pode ser realizada por Bháskara, ou ainda quando o coeficiente ![]() , usando a resolução como uma expressão matemática.
, usando a resolução como uma expressão matemática.
Para ![]()
Uma equação do 2º grau com coeficiente ![]() , é representada como
, é representada como ![]() . A expressão
. A expressão ![]() é um exemplo.
é um exemplo.
Neste caso:
Coeficiente ![]()
Coeficiente ![]()
Coeficiente ![]()
E a sua resolução é dada por:
![]()
![]()
![]()
![]()
As raízes desta equação do 2º grau ![]() são -3 e 3, e sua representação gráfica é:
são -3 e 3, e sua representação gráfica é:
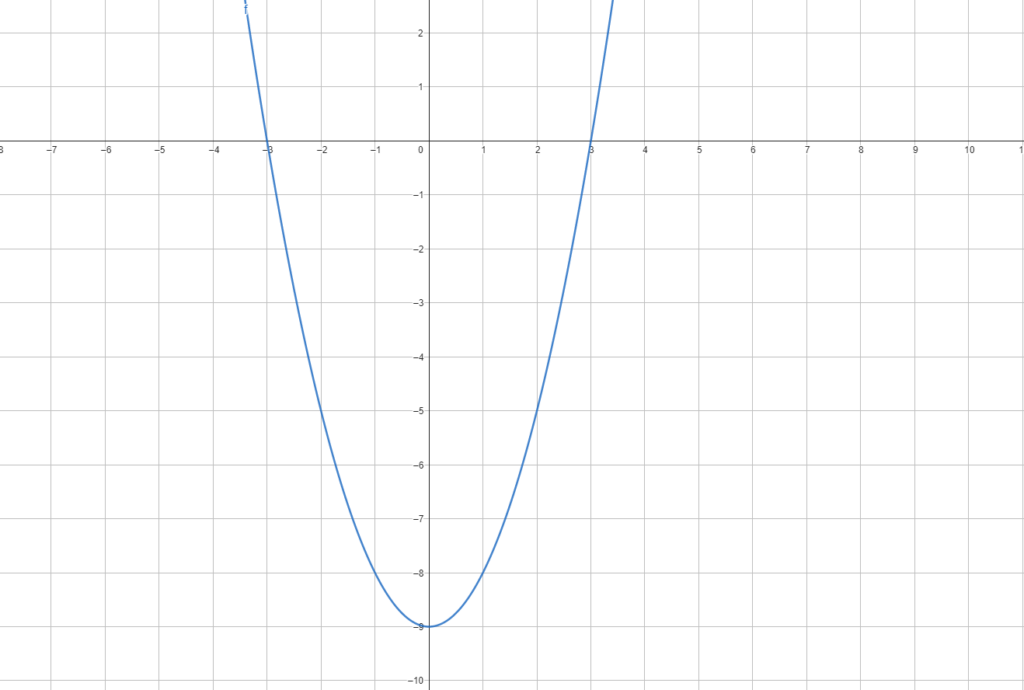
Para ![]()
A resolução de uma equação do 2º grau com coeficiente ![]() , é representada como
, é representada como ![]() . A expressão
. A expressão ![]() é um exemplo, e a sua resolução requer a aplicação da fórmula de Bháskara, ou ainda pode ser resolvida por meio da soma e produto.
é um exemplo, e a sua resolução requer a aplicação da fórmula de Bháskara, ou ainda pode ser resolvida por meio da soma e produto.
Neste caso:
Coeficiente ![]()
Coeficiente ![]()
Coeficiente ![]()
Fazendo a resolução por Bháskara teremos:
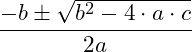
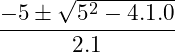
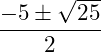
![]()
![]()
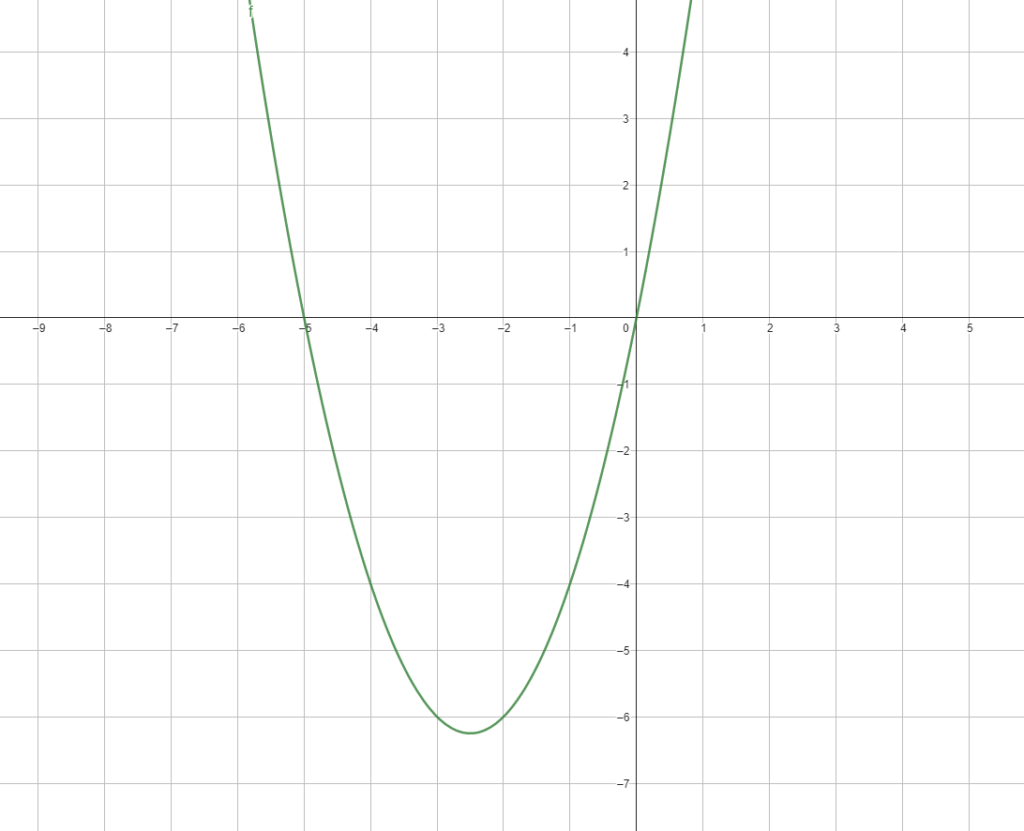
As raízes desta equação do 2º grau incompleta ( ![]() ) iguais a
) iguais a ![]() e
e ![]() e sua representação gráfica será:
e sua representação gráfica será:
Para ![]() e
e ![]()
A resolução de uma equação do 2º grau com os coeficientes ![]() e
e ![]() , é zero, pois como
, é zero, pois como ![]() , tanto na resolução pela fórmula de Bháskara, ou ainda pode ser resolvida por meio da soma e produto encontraremos as raízes de
, tanto na resolução pela fórmula de Bháskara, ou ainda pode ser resolvida por meio da soma e produto encontraremos as raízes de ![]() .
.
Exercícios
ENEM – exercícios
REsolução
ENEM – Exercício
Resolução
Continua depois da publicidade
