Dízimas periódicas: fração geratriz

ChatGPT: será o fim dos professores de redação?

31 de janeiro de 2023

Anti-ChatGPT já está disponível

3 de fevereiro de 2023

1 de fevereiro de 2023

(EF08MA05) Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.

Dízima Periódica
Tipos de dízimas periódicas
Fração Geratriz

Dízima periódica

Neste momento dos seus estudos certamente você já se deparou com divisões que não apresentam um resultado exato, pois geram infinitas casas decimais.

Esse número decimal com infinitas casas decimais e periódicas, é o que se define como Dízima periódica.

$\dfrac{1}{3}=0,3333333.....$

Um exemplo é a divisão do numeral 1 (numerador) pelo 3 (denominador), que tem como resultado o valor de 0,3333…. com infinitas casas decimais em que o 3 se repete.

Período de uma dízima periódica: define-se de período os algarismos que se repetem nela. Como no exemplo acima, o período é o algarismo 3. Já em 22,53636363636 o período são os algarismos 36, enquanto o algarismo 5 é definido como antiperíodo.

Conheça nossos planos de aulas online

Atenção

As dízimas periódicas são classificas em simples e compostas, como veremos a seguir. Mas também temos as dízimas não periódicas.

As dízimas periódicas apresentam um período, ou seja, possuem uma mesma sequência de repetição e fazem parte do conjunto dos números racionais. Como o exemplo acima de 1/3=0,3333….

Já as dízimas não periódicas são aquelas que não apresentam uma repetição dos números decimais, e portanto fazem parte do conjunto dos números irracionais. Como por exemplo:

√2 = 1,414213562373….
√3 = 1,732050807568….
√7 = 2,645751311064…

Tipos de dízimas periódicas

Dízima periódica simples

Caracterizada por não possuir um antiperíodo, ou seja, o número que se repete infinitamente vem logo depois da vírgula. Como por exemplo:

$\dfrac{1}{3}=0,3333333.....$

parte inteira= 0
período = 3

$\dfrac{2}{3}=0,666666.....$

parte inteira = 0
período = 6

Dízima periódica composta

Como o próprio nome sugere, uma dízima periódica composta possui além da parte inteira (antes da vírgula), uma parte não periódica e o próprio período.

1,68888
1 – parte inteira
6 – parte não periódica
8 – parte periódica

Fração Geratriz

Define-se de fração geratriz é a fração que gera uma dízima periódica. Porém, encontrá-la nem sempre é uma tarefa fácil. Mas normalmente é possível encontrá-la pelo método prático.

Fração Geratriz de Dízimas Periódicas Simples

Exemplo:
Vamos encontrar a fração geratriz da dízima periódica 0,333333333

1º passo: iguale a dízima a uma variável, como o “x”

$x = 0,333333333....$

2º passo: multiplique os dois lados da equação de acordo com o número de algarismos do período:
10 – se houver apenas 1 algarismo no período
100 – se houver 2 algarismos
1000 – se houver 3 algarismos,
e assim sucessivamente.

no nosso exemplo, a multiplicação será por 10

$x \times 10 = 0,333333333 \times 10$

$10 \cdot x = 3,333333333$

3º passo: Calcule a diferença entre a equação encontrada no 2º passo e a do 1º passo.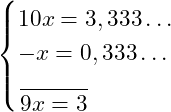

$\begin{cases}10x=3,333\ldots \\ -x=0,333\ldots \\ \dfrac{}{9x=3}\end{cases}$

O resultado da subtração será:

$10 \cdot x - x = 3,333 - 0,333$
$9 \cdot x = 3$

$x=\dfrac{3^{\div 3}}{9^{\div 3}}=\dfrac{1}{3}$

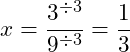
Exemplo 2: vamos ver agora o exemplo de uma fração geratriz de um número maior do que 1 ( > 1 ), como o 12,3333333….

1º passo: neste caso o primeiro passo é separar a parte inteira do decimal:

12 + 0,3333333

E então encontrar a fração geratriz da parte decimal. Como utilizamos o mesmo decimal do exemplo 1, já sabemos que esta fração é igual a $=\dfrac{1}{3}$

Agora basta somar a parte inteira com a fração encontrada, lembrando que será necessário encontrar o MMC.

$12+0,333\ldots$

$12+\dfrac{1}{3}$

$\dfrac{12}{1}+\dfrac{1}{3}=\dfrac{36+1}{3}=\dfrac{37}{3}$

Fração Geratriz de Dízimas Periódicas Composta

Um outra situação que podemos nos deparar, é com a necessidade de encontrar a fração geratriz de uma dízima periódica composta, ou seja, aquela que possuí um antiperíodo.

Neste caso o procedimento segue a mesma lógica da fração geratriz de uma dízima periódica simples, contudo, devemos lembrar que o objetivo é sempre “eliminar” todo o período.

Exemplo: Vamos encontrar a fração geratriz do número 1,36171717…

1º passo: para deixarmos apenas um período simples após a vírgula (como números decimais), precisaremos multiplicar por 100, assim todos os números que não se repetem estarão na frente da vírgula:

$\begin{cases}x=1,36171717\ldots \\ \dfrac{\times 100}{100x=136,171717\ldots }\end{cases}$

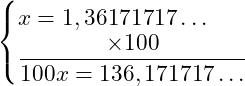
2º passo: agora vamos repetir o passo anterior, porém multiplicando por 10.000, pois assim conseguimos passar além do antiperídodo também o período para frente da vírgula. Assim:

$\begin{cases}x=1,36171717\ldots \\ \dfrac{\times 10.000}{10.000x=13617,171717\ldots }\end{cases}$

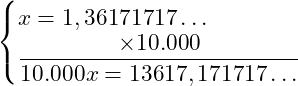
3º passo: agora vamos subtrair a equação encontrada no 1º passo da expressão encontrada no 2º passo:

$\begin{cases}10.000x=13617,171717\ldots \\ \dfrac{-100x=136,171717\ldots }{9.900x=13.481}\end{cases}$

$x=\dfrac{13.481}{9.900} = x=1,36171717\ldots$

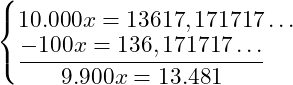
Assim encontramos a equação geratriz da dízima 1,36171717…. = $x=\dfrac{13.481}{9.900}$

Continua depois da publicidade

Exercícios

ENEM – exercícios

Resolução

REsolução

ENEM – Exercício

Resolução

Continua depois da publicidade

Gostou deste conteúdo? Compartilhe agora mesmo!

Fernando Pitt

Engenheiro, Mestre, Professor, Educador, e um entusiasta de tecnologia.

Dízimas periódicas: fração geratriz

ChatGPT: será o fim dos professores de redação?

Anti-ChatGPT já está disponível